Reranking en RAG : améliorer la précision grâce aux cross-encodeurs

Le reranking s’impose désormais comme un élément essentiel dans l’architecture technique de la génération augmentée par récupération (RAG). Cette méthode puissante permet de réorganiser les résultats dès la première phase de la recherche, optimisant ainsi de manière significative la précision des réponses obtenues.

Pour bien appréhender le reranking, il est nécessaire de comprendre le rôle des encodeurs, en particulier des bi-encodeurs et des cross-encodeurs. Ces deux approches jouent un rôle clé dans l’évaluation et le tri des résultats, contribuant à une amélioration notable des performances globales.

Encodeur

Commençons par expliquer brièvement ce qu’est un encodeur. Depuis l’introduction de l’architecture transformer [Vaswani et al., 2017], un encodeur de texte fait souvent référence à un transformer de type encodeur uniquement, tel que BERT [Devlin et al., 2019]. Il est constitué d’un tokenizer, d’une couche d’embedding, puis de couches composées de réseaux feed-forward et de mécanismes d’attention. Le mécanisme d’attention prend en compte le contexte à gauche et à droite dans toutes les couches, ce qui permet de capturer les dépendances entre les tokens. Ce design permet au modèle de construire des représentations contextuelles riches du texte d’entrée, ce qui est essentiel pour de nombreuses tâches de traitement du langage naturel (NLP), y compris le reranking.

Bi-encodeur

Architecture du bi-encodeur

L’architecture du bi-encodeur se compose de deux encodeurs séparés (en pratique, il s’agit souvent du même encodeur utilisé deux fois). Ces deux encodeurs créent deux représentations compressées de la requête et du passage : $r_q$ et $r_p$. Pour calculer le score de pertinence entre la requête et le passage, une fonction de similarité $s$, telle que le produit scalaire $s(r_q,r_p) = \langle r_q, r_p \rangle$ ou la similarité cosinus $s(r_q,r_p) = \frac{\langle r_q, r_p \rangle}{||r_q||.||r_p||}$, est appliquée.

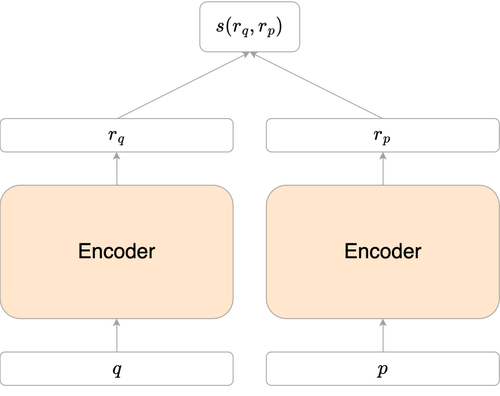
Entrainement du bi-encodeur

L’entraînement d’un modèle bi-encodeur vise à maximiser la similarité entre la requête et le passage pertinent tout en minimisant la similarité entre la requête et les passages non pertinents. Cela est souvent réalisé à l’aide d’une fonction de perte contrastive, qui encourage le modèle à rapprocher les paires pertinentes dans l’espace d’embedding et à éloigner les paires non pertinentes.

Dans le cas d’un passage pertinent et de plusieurs passages non pertinents, la perte contrastive $\mathcal{L}$ peut être exprimée comme suit :

$$\mathcal{L}(q, p^+, (p_i^-)_i) = - \log \left( \frac{e^{\text{sim}(q, p^+)}}{e^{\text{sim}(q, p^+)} + \sum_{i=1}^n e^{\text{sim}(q, p_i^-)}} \right)$$

S’il y a plusieurs passages pertinents et plusieurs passages non pertinents, cela devient :

$$\mathcal{L}(q, (p_j^+)_j, (p_i^-)_i) = - \log \left( \frac{\sum_{j=1}^m e^{\text{sim}(q, p_j^+)}}{\sum_{j=1}^m e^{\text{sim}(q, p_j^+)} + \sum_{i=1}^n e^{\text{sim}(q, p_i^-)}} \right)$$

où

• $q$ est la représentation vectorielle de la requête.
• $p^+$ est la représentation vectorielle des passages positifs (pertinents).
• $(p_i^-)_i$ sont les représentations vectorielles des passages négatifs (non pertinents)
• $(p_j^+)_j$ sont les représentations vectorielles des passages positifs (pertinents), s’il y a plusieurs passages positifs.
• $\text{sim}(q, p)$ est le score de similarité entre la requête $q$ et la représentation vectorielle du passage $p$ (généralement un produit scalaire ou une similarité cosinus).
• $n$ est le nombre d’échantillons négatifs.
• $m$ est le nombre d’échantillons positifs, s’il y a plusieurs échantillons positifs.

Bi-encodeur : avantages et inconvénients

L’un des principaux avantages des bi-encodeurs est leur efficacité. Étant donné que les encodages de la requête et du passage peuvent être précalculés de manière indépendante, la phase de récupération nécessite uniquement un calcul de similarité simple, qui est presque instantané. Cela rend les bi-encodeurs très évolutifs, particulièrement adaptés aux tâches de récupération à grande échelle où des millions de passages peuvent devoir être pris en compte.

Cependant, l’inconvénient est que l’architecture des bi-encodeurs peut manquer certaines interactions fines entre la requête et le passage, car les représentations sont créées indépendamment. Cette limitation peut entraîner une précision inférieure dans les cas où des nuances sémantiques subtiles sont importantes.

Voyons un autre encodeur capable de capturer des interactions fines entre la requête et le passage.

Cross-encodeur

Architecture du cross-encodeur

Contrairement au bi-encodeur, l’architecture du cross-encoder combine la requête et le passage en entrée dans un seul transformer BERT. Le mécanisme d’attention est appliqué sur les tokens des deux séquences de manière conjointe, ce qui permet au modèle de capturer des interactions plus riches entre la requête et le passage. Cette architecture est connue sous le nom de modèle d’interaction car elle modélise explicitement l’interaction entre les deux entrées à chaque couche du transformer.

Le fait que le mécanisme d’attention soit capable de s’atteler à la fois à la requête et au passage améliore considérablement la précision.

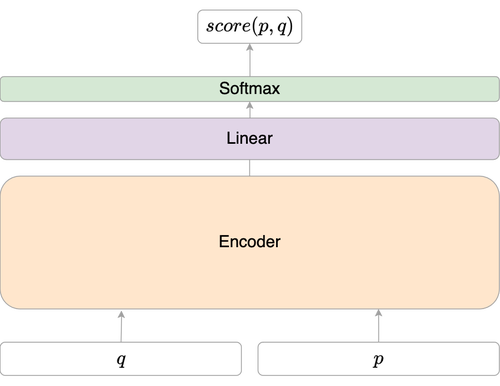
Ainsi, un cross-encoder est essentiellement un encodeur suivi d’un classificateur. Cependant, nous devons l’entraîner. Voyons comment.

Entrainement du cross-encodeur

Les cross-encodeurs sont également entraînés pour maximiser et minimiser la similarité entre les paires de requêtes-passages pertinentes et non pertinentes. Pour ce faire, on utilise la perte d’entropie croisée binaire (BCE), qui peut être exprimée comme suit :

$$ \mathcal{L} = - \left( y \cdot \log(\hat{y}) + (1 - y) \cdot \log(1 - \hat{y}) \right) $$

où

• $y$ est l’étiquette vraie (1 pour pertinent, 0 pour non pertinent).
• $\hat{y}$ est la probabilité prédite que le passage soit pertinent.

Cette fonction de perte encourage le modèle à produire une probabilité plus élevée pour les paires de requêtes-passages pertinentes et une probabilité plus basse pour les paires non pertinentes.

Cross-encodeur : avantages et inconvénients

La capacité du cross-encoder à modéliser les interactions entre les tokens de la requête et du passage permet d’obtenir une grande précision, en particulier dans les tâches nécessitant une compréhension nuancée.

Cependant, le besoin de recalculer l’encodage pour chaque paire de requêtes-passages rend les cross-encodeurs intensifs en termes de calcul, en particulier lorsqu’on travaille avec de grands ensembles de données. Cela limite leur évolutivité par rapport aux bi-encodeurs.

En effet, si vous avez une requête $q$ et certains passages $P$.

• Un bi-encodeur encoderait $q$ et le comparerait aux encodages de passages précalcules $|P|$. Ainsi, lors de l’inférence, il nécessite un forward pass de l’encodeur.
• Un cross-encoder encoderait chaque paire $(q, p), p \in P$. Ainsi, lors de l’inférence, il nécessite $|P|$ un forward pass du cross-encoder.

Compromis entre scalabilité et précision

Pour tirer le meilleur parti des deux mondes, une approche courante consiste d’abord à effectuer une recherche vectorielle à l’aide d’un bi-encodeur, qui réduit rapidement le nombre de passages candidats. Les meilleurs candidats issus de cette étape de récupération sont ensuite réévalués à l’aide d’un cross-encodeur, offrant un équilibre entre scalabilité et précision.

Encore mieux, vous pouvez combiner d’autres techniques de récupération, telles que BM25. Cette approche hybride tire parti des forces de différents modèles et évite la nécessité d’une formule de fusion comme la Fusion de Rang Réciproque (RRF), qui mixe les scores de plusieurs modèles de récupération.

Conclusion

Le reranking dans une stack RAG combine efficacement la malléabilité des bi-encodeurs avec la précision des cross-encodeurs, offrant un outil puissant pour améliorer la pertinence des informations récupérées. En ce sens, il joue un rôle crucial dans les systèmes modernes de récupération d’information et de traitement du langage naturel.

Références

• Passage Re-ranking with BERT [en]
• Re2G: Retrieve, Rerank, Generate [en]
• Reciprocal Rank Fusion outperforms Condorcet and individual Rank Learning Methods [en]
• BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding [en]
• Attention Is All You Need [en]

Pour aller plus loin

• ColBERT: Efficient and Effective Passage Search via Contextualized Late Interaction over BERT [en]
• What is ColBERT and Late Interaction and Why They Matter in Search?, Jina [en]
• Late Chunking in Long-Context Embedding Models [en]
• Hybrid Search Revamped [en]